Trong nội dung chúng tôi chia sẻ cho các bạn đọc trong bài viết này là những kiến thức Hình Học về trọng tâm, đường trung tuyến của tam giác. Để các bạn hiểu rõ hơn trọng tâm là gì? Đường trung tuyến là gì? Công thức tính và có những ví dụ cụ thể để các bạn học sinh của chúng ta nắm vững kiến thức.
Những kiến thức về đường trung tuyến của tam giác
Trung tuyến là gì?
Định nghĩa đường trung tuyến: Đường trung tuyến của một đoạn thẳng là một đường thẳng đi qua trung điểm của của đoạn thẳng đó.
Đường trung tuyến của tam giác là gì?
Đường trung tuyến của tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện. Mỗi tam giác sẽ có 3 đường trung tuyến.
Tính chất đường trung tuyến trong tam giác
- Ba đường trung tuyến của tam giác cùng đi qua một điểm. Và điểm đó sẽ cách đỉnh 1 khoảng bằng 23 độ dài đường trung tuyến đi qua đỉnh đó.
- Giao điểm của 3 đường trung tuyến được gọi là trọng tâm.
- Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 23 độ dài đường trung tuyến đi qua đỉnh đó.
Ví dụ: Cho tam giác ABC, gọi N là trung điểm của AB, M là trung điểm của AC, I là trung điểm của BC. Theo như hình dưới.
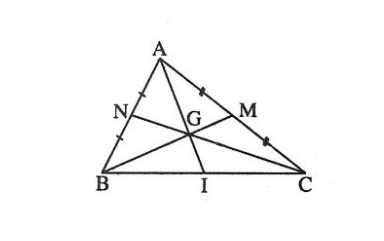
Vậy theo hình ta có:
-
- Trung tuyến của tam giác ABC sẽ là: AI, BM và CN
- Theo tính chất đường trung tuyến ta có: AI, BM và CN sẽ đi qua một điểm gọi là điểm G.
- G = là trọng tâm của tam giác ABC
- Trọng tâm G cách mỗi đỉnh bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó. Tức ta sẽ có một biểu thức như sau: AGAI=BGBM=CGCN=23
Những kiến thức về trọng tâm của tam giác?
-
Trọng tâm là gì?
Trọng tâm của tam giác là gì? Trọng tâm trong tam giác là giao điểm của ba đường trung tuyến xuất phát từ ba đỉnh của tam giác đó.
Tức 3 đường trung tuyến của một tam giác đồng quy tại một điểm. Điểm đó được gọi là trọng tâm của tam giác.
-
Tính chất trọng tâm của tam giác
Tính chất trọng tâm trong tam giác là khoảng cách từ trọng tâm tới 3 đỉnh của tam giác bằng 23 độ dài đường trung tuyến ứng với đỉnh đó.
Ví dụ: Cho tam giác ABC, gọi N là trung điểm của AB, M là trung điểm của AC, I là trung điểm của BC. Ta được hình như sau:
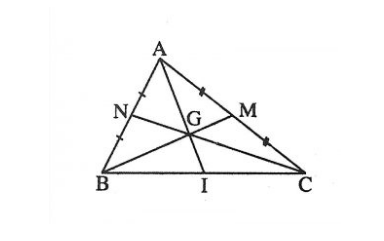
Ta dễ dàng thấy được: AI, BM, CN đồng quy tại một điểm. Ta đặt điểm đó là điểm G. Vậy G chính là trọng tâm của tam giác ABC.
Theo tích chất về trọng tâm hình tam giác thì ta có: AG= 23 AI, BG= 23 BM, CG=23CN.
-
Trọng tâm của các hình học đặc biệt
Để xác định được trọng tâm của tam giác thì ta hãy đi theo một ví dụ dưới đây.
Cho tam giác ABC, gọi: M là trung điểm của AC, sao cho MA=MB
N là trung điểm của AB, Sao cho NB=NA
I là trung điểm của BC, sao cho IB=IC
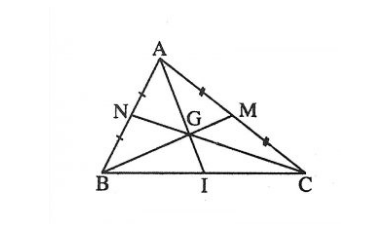
Xác định trọng tâm của tam giác ABC bằng cách
- Nối A với I, ta được trung tuyến AI
- Nối B với M, ta được trung tuyến BM
- Nối C với N, ta được trung tuyến CN
- Suy ra giao 3 đường trung tuyến AI, BM, CN tại 1 điểm, ta gọi là điểm G. Vậy theo tính chất trọng tâm của tam giác thì G là trọng tâm của tam giác ABC
-
Trọng tâm của tam giác cân
Trọng tâm tam giác cân cũng được tìm theo như tam giác bình thường khác. Tuy nhiên đây là hình dạng đặc biệt nên ta xét trường hợp tam giác ABC cân tại A. G sẽ là trọng tâm của tam giác ABC. Vì cân tại A nên AG vừa là đường trung tuyến vừa là đường cao và là đường phân giác của tam giác ABC.
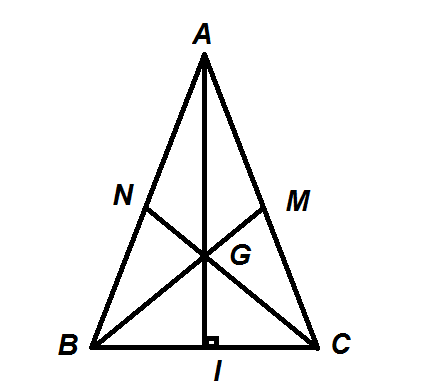
Ta có: AG vuông góc với BC
Tam giác ABI và tam giác ACI vuông tại I.
-
Trọng tâm của tam giác vuông
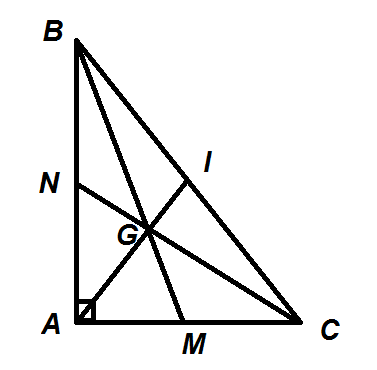
Trọng tâm tam giác vuông cũng được tìm như cách tìm trọng tâm tam giác thường. Ta xét tiếp trường hợp tam giác ABC vuông tại A. G là trọng tâm của ABC.
Vì AI là trung tuyến của 1 góc vuông nên ta có AI = 12 BC. Tức AI = BI = CI.
- Tam giác AIB cân tại I, và tam giác AIC cân tại I.
-
Trọng tâm của tam giác vuông cân
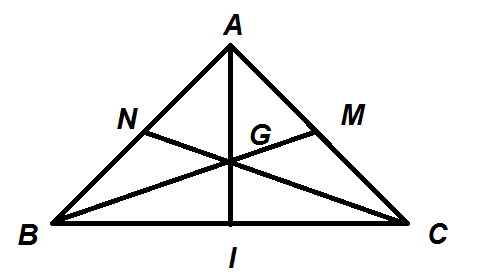
Trọng tâm tam giác vuông cân cũng được xác định như tam giác thường. Xét tam giác ABC vuông cân tại A. G là trọng tâm của tam giác ABC. Vì tam giác vuông cân tại A nên AG là đường trung tuyến, đường trung trực, đường cao của tam giác ABC => AG vuông BC
Ngoài ra còn có: AB = AC (Cân tại A) => BM=BN
BN= AN=AM=CM
Tóm lại: Đối với những kiến thức về trọng tâm là gì, đường trung tuyến là gì, trọng tâm của tam giác xác định như thế nào… thì đây là những kiến thức mà các bạn có thể tìm thấy trong sách giáo khoa lớp 7. Với những chia sẻ trên chắc chắn sẽ giúp bạn nhớ lại những điều vô cùng hữu ích về toán hình học.
Tuy nhiên lượng kiến thức này sẽ được nhắc lại trong bộ môn hình học được học vào năm 10 khi các bạn học về tọa độ trọng tâm tam giác. Lúc đó sẽ còn rất nhiều các công thức trọng tâm tam giác khó và phức tạp hơn rất nhiều.
Vậy nên qua những chia sẻ này chúng tôi muốn các bạn nắm vững kiến thức về các đường trong tam giác, các tính chất trọng tâm tam giác. Đặc biệt nắm vững định nghĩa về trọng tâm của tam giác để áp dụng giải các bài tập hình học dễ dàng hơn.
>> Tham khảo thêm: Nguyên âm là gì? Phụ âm là gì? Cách phân biệt nguyên âm và phụ âm
>> Tham khảo thêm: Số nguyên tố là gì? Hợp số là gì? Tổng hợp kiến thức liên quan